高度計算機はHPCテックにお任せください。

  • トップページ
  • 製品案内
  • 導入事例
  • 会社情報
  • サポート
  • お取引・お問い合わせ
03-5643-2681
お問い合わせ
English

導入事例

2013/04/01

[導入事例] 東京理科大学 仁木 直人先生、飯田 正成先生

東京理科大学 仁木 直人先生、飯田 正成先生にGPU搭載計算機を導入頂きました。

研究内容

東京理科大学 工学部 経営工学科 仁木研究室

 

研究分野

数式処理／統計学／計算機科学

 

研究概要

計算機を使った数学や統計学（数式処理、計算機統計学，統計量分布論）、数学・統計学研究に必要な計算（数値数式混合計算、記号処理、確率的計算）、数学的基礎を持った情報の取り扱い（数理情報学）などを研究対象としています。
応用を意識した基礎研究を中心とした研究室ですが、学生は、様々なシステムの開発、自分の興味ある分野での調査と統計データ解析、統計的シミュレーションによる計算機内実験など、計算機と情報の利用に関わる幅広い範囲を研究しています。たとえば、

  1. 対称式基底変換算法と統計量分布論への応用
  2. 状態空間表現を用いた時系列モデル
  3. サイト内検索における補助機能開発と効果検証

などです。

導入システム

今回弊社からGPU搭載計算機を導入頂きました。

仁木研究室では、GPUがどのような統計計算に向くか考察・検討した結果、CPU比100倍という大変な高速化を実現されました。

MCMCへの応用

MCMC (Markov Chain Monte Calro) 法を用いて、分割表の正確確率検定における p 値を CPU単独とGPUで計算した時の比較。

分割表の独立性に関する正確確率検定のp 値計算にMCMC 法の一種であるメトロポリス法を用いた時の実時間例をTable 1. に示す。ただし、計測に用いた分割表は、

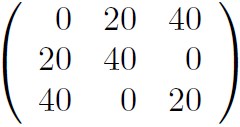
のように、公差20 の等差数列を巡回した行および列から成り、繰返し回数は4, 096 × 1015 である。また、素朴な計算法では1 ステップ毎に対数関数を32 + 1 ∼ 72 + 1 回呼んでいるのに対して、教科書的計算法では5 回呼んでいる。簡単な工夫により、対数関数の呼出しはさらに減らすことができるが、比の値は20 倍程度とあまり変わらない。

    1. モンテカルロ計算など、独立した同じ演算の繰返しが多数行われる問題に適用したこと。このとき、各スレッドに割付ける手続き数（繰返し回数は確率変動）を大きくすることで、SIMD 計算のオーバーヘッドを解消している。

 

    1. 高速なレジスタとシェアドメモリを用いた計算を行って、低速なグローバルメモリの使用を必要最低限としたこと。多くの問題で、上記項目の1と2 により、20 倍程度の高速化が可能。

 

    1. 統計計算に多出する対数関数・べき乗などの初等関数を SFU (Super Function Unit)を用いて高速計算していること(→ MCMC) 。SFU による計算は、C の標準ライブラリを用いた場合よりも、100 倍以上早いのが大きな魅力。

 

  1. 条件分岐によるパイプライン停止を起こし難い GPU の特性が生きる場合には、思った以上の高速化が生じること (→ ランダムウォーク)
 Table 1.
MH法 MH法の実計算時間例(sec)
計算法 分割表 GPU CPU 比
素朴 3×3 6.63 692.2 104.4
5×5 18.36 1831.8 99.8
7×7 33.97 3500.5 103.1
教科書的 3×3 3.12 142.3 45.6
5×5 7.75 182.5 23.6
7×7 12.81 345.5 19.2

ランダムウォークへの応用

原点から出発して、数直線上を確率1/2 で左または右に 1 だけ移動するランダムウォークが、±D に設定された境界に到達する時間分布を数値的に求めるシミュレーションを行ったとき、要した実時間をFigure 1.に示す。ただし、4,096のスレッドを用い、到達時間の総計測回数はいずれも4, 096 × 105 回である。また、凡例にある1 ∼ 105 の数字は、各ワープにおいてスレッド間同期をとる単位計測回数を示す。すなわち、それが104 なら、各スレッドで10 回ワープ内同期をとって計算されたことになる。

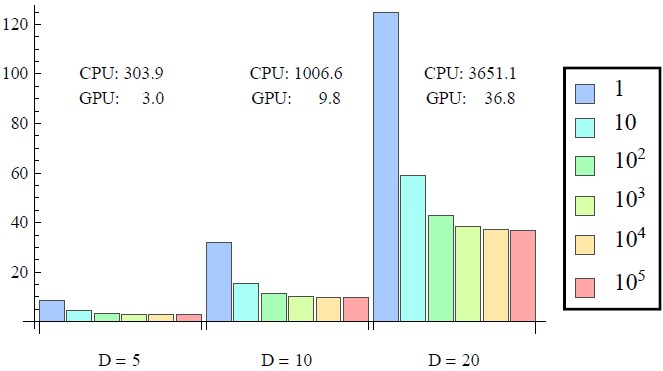
Figure 1. Random walk の境界到達時間計測に要した実時間例(sec)

Figure 1. Random walk の境界到達時間計測に要した実時間例(sec)

今後の展望

上記データにおけるスペックとして、CPU は Intel Core i7 (3.4GHz)、GPU は NVIDIA Tesla C2070 を使用しています。なお、今回の高速化は他の同様な計算にも十分適用可能です。

 

仁木先生コメント「統計計算における GPGPU は実用性が高いと思う。Mathematica （バージョン 8.0.4）を用いた GPGPU 計算の前後処理は大変便利だが、Windows の下でないとあまりうまく動かない。Cent OS 下でのバージョン 9 はこれから試す」

 

とのことでした。

最後に

大変興味深い研究に当社製品・サービスを有効に活用いただき、心より感謝申し上げます。ありがとうございました。

（左）飯田 正成先生 （右）仁木 直人先生

研究室URL http://nikilab.ms.kagu.tus.ac.jp/indexj.html

東京理科大学　仁木 直人先生の略歴

1971年 東京大学 工学部卒業

1971年 文部省統計数理研究所第四研究部研究員に就任

1983年 文部省統計数理研究所第四研究部第一研究室長に就任

1985年 文部省統計数理研究所統計データ解析センター データ解析室長に就任 (予測制御系統計計算システム研究部門助教授を併任)

1987年 九州大学理学部付属基礎情報学研究施設助教授に就任 (大学院総合理工学研究科情報システム学専攻助教授を併任)

1993年 東京理科大学工学部第一部経営工学科教授に就任

 

飯田 正成先生は2013年4月より東京理科大学塩濱研究室にて研究活動に従事されるご予定です。

主な著書

「基礎情報学」培風館(2009年) Amazonへのリンク

所属学会

Internationa Statistical Institute (elemented member)

International Association for Statistical Computing

Association for Computing Machinery

ACM SIG for Symbolic and Algebraic Computation

日本統計学会

日本計算機統計学会

数式処理学会 など

弊社では、科学技術計算や解析などの各種アプリケーションについて動作検証を行い、
すべてのセットアップをおこなっております。

お客様が必要とされる環境にあわせた最適なシステム構成をご提案いたします。

各種カスタマイズ・詳細なお見積はこちらからお問い合わせください。

導入事例

Page Top

(c) 2012- HPCTECH All Rights Reserved