導入事例
2016/08/29
[導入事例] 東京工業大学 横田研究室 様
Intel Xeon Phi Processor(Knights Landing)搭載ワークステーションを導入いただきました。
研究内容

東京工業大学 横田理央准教授にお話を伺いました。
研究室の紹介
横田研究室様は2016年4月にスタートした新しい研究室で、次世代スーパーコンピュータのための
基盤ソフトウェア・アルゴリズムの開発をされています。また、そのための並列性の抽出、通信量の低減、負荷分散、自動最適化などの研究もされています。
研究内容の紹介
▶ N体問題
N体問題は重力多体問題や分子動力学などの物理現象自体が離散的な点の相互作用で記述される分野で盛んに用いられてきました。しかし、N体問題の解法は弾性力学、流体力学、電磁気学、音響学、量子力学などの数値解析にも用いることができます。これは連続体を記述する偏微分方程式を積分方程式に変換し求積点を用いて積分を行うことで離散点同士の相互作用問題に帰着するためです。そのため、N体問題の高速解法は科学技術計算において欠かすことのできないアルゴリズムであるといえます。
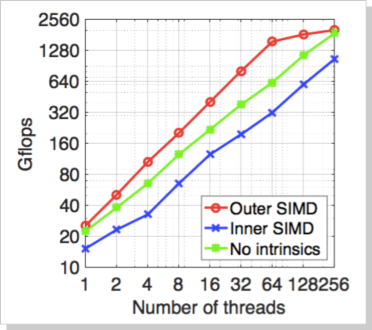
下図に Knights Landing における N体問題のスケーラビリティを GFlops で示します。256スレッドを用いた計算では単精度 2TFlops を超える演算性能が得られました。積和演算以外の演算を多数含む N体問題のカーネルとしてはまずまずの性能であるといえます。このコードは Knights Corner 用に最適化してあったコードをほぼそのまま用いました。「Outer SIMD」はイントリンシックを使って外側のループを SIMD 化したものであり、「Inner SIMD」はイントリンシックを使って内側のループを最適化したもの、「No intrinsics」はイントリンシックを用いずに普通の C コードをコンパイラに SIMD 化を任せたものです。
▶ 高速多重極展開法
高速多重極展開法 (FMM) は N 体問題の計算コストを O(N2) から O(N) に軽減する手法です。FMM は FFT や Krylov 部分空間法などと並んで20世紀の10大アルゴリズムの一つと考えられています。通常 Byte/flop の低い密行列などのアルゴリズムはその複雑性が高く O(N3)、複雑性の低い FFT や疎行列計算などのアルゴリズムは Byte/flop が高くなります。しかし、FMM は O(N) の複雑性も有しながらも密行列積よりも低い Byte/flop を実現できます。つまり、FMM は効率的なアルゴリズムでありながらも演算密度が高く、次世代の計算機アーキテクチャにおける様々な楕円型方程式の高速解法の代替手法として期待されています。
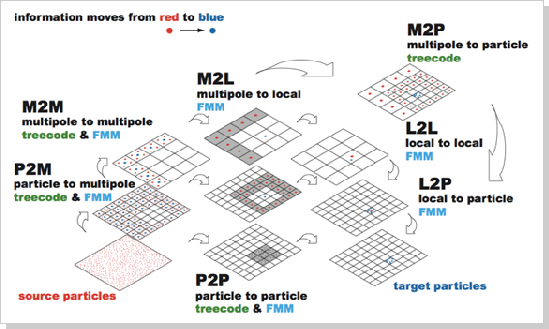
図1 FMMの計算の流れ
N体問題の計算を高速化する手法として FMM は非常に有効です。FMM は6つの部分から成り立っています。P2M は粒子の情報から多重極展開への変換、M2M は多重極展開から多重極展開での変換、M2L は多重極展開から局所展開への変換、L2L は局所展開から局所展開への変換、L2P は局所展開から粒子の作用への変換、P2P は粒子同士の直接相互作用を表します。また、treecode は FMM と異なり、M2L、L2L、L2P の代わりに M2P の変換を行うことで多重極展開から粒子での直接の作用を計算します。
▼クリックすると拡大します。
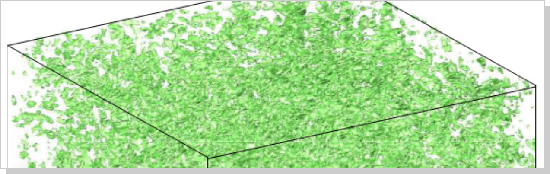
図2 タンパク質のクラウディング分子シミュレーション
分子動力学による解析は一般的に水で満たされた周期境界条件のような理想化された試験環境下 (in vitro) で行われます。一方、実際の細胞などは様々なタンパク質が混在しており、そのような環境下での挙動を in vitro の計算から予測するには限界があります。本研究では 663,552 コアを用いた並列計算で5億原子の分子シミュレーションを行い、タンパク質が受けるクラウディングの影響を調べました。
▼クリックすると拡大します。
図3 境界要素法を用いた暗溶媒による分子シミュレーション
分子シミュレーションは水分子を陽的に扱う陽溶媒と、連続体として扱う暗溶媒があります。暗溶媒の場合は分子の表面を境界要素法で離散化し、その上で積分方程式を解くことでポテンシャル場や力場の解析を行います。図3に示すように大規模解析においては多数の分子の集まりを境界要素法でそれぞれ離散化し、まとめて解くことで分子が混在するような場を解析することができます。
▼クリックすると拡大します。
図4 渦法を用いた一様等方性乱流の解析
乱流解析も渦を最小単位とするような離散化を行うことで N 体問題として解くことができます。これにより、FMM を用いて Poisson 方程式に相当する部分を O(N) の計算時間で解くことができ、大規模並列計算において良いスケーリングを得ることができます。
東京工業大学 学術国際情報センター 横田研究室 ホームページ
http://www.rio.gsic.titech.ac.jp/jp/
導入システム

導入システムの狙いや目的を教えてください
Intel Xeon Phi Processor(開発コード名:Knights Landing)が発売された事を知り、これからの開発に使用する為に導入をしました。通常は大規模クラスター型スーパーコンピュータ『TSUBAME』を使用していますが、次世代スーパーコンピュータ『メニーコア型大規模スーパーコンピュータシステム』には Intel Xeon Phi Processor を搭載することもあり、開発生産性などを手元の計算機で確認する為に最適だと思い導入いたしました。また、『FMMとH行列を組み合わせた大規模連立一次方程式の反復解法』や『H行列を用いた深層学習における密行列積の高速化』の研究などにも使えたらと思っています。この計算機の導入にあたり OS やコンパイラのインストールをHPCテックさんに行ってもらいましたので、直ぐに使用する事が出来ました。
本格的に使用するのはこれからですが、Intel Xeon Phi Processor (Knights Landing) では 16GB のオンパッケージメモリが搭載されている事や Knights Corner に比べて改善された部分が多く、どのくらい性能が出るのかこれから検証してみたいと思います。